

With spherical coordinates, we can define a sphere of radius r by all coordinate points where 0 ≤ ϕ ≤ π (Where ϕ is the angle measured down from the positive z axis), and 0 ≤ θ ≤ 2 π (just the same as it would be polar coordinates), and ρ = r ). b) Calculate the volume and surface area of a cylinder of radius R and length L using integration method. The solid angle subtended by the surface area of an entire sphere with a radius of r can be computed as follows: spere4r2r24 sr. Over 2200 years ago Archimedes proved that the surface area of a spherical cap is always equal to the area of a circle whose radius equals the distance from the rim of the spherical cap to the point where the caps axis of. This solution looks long because I have broken down every step, but it can be computed in just a few lines of calculation The above is found by computing the following double integral using the unit surface element in spherical coordinates. When the sphere has unit radius, it is usual to call it the unit n-sphere or simply the n-sphere for brevity.It is easier to use Spherical Coordinates, rather than Cylindrical or rectangular coordinates. Spherical coordinates of the system denoted as (r,, ) is the coordinate system mainly used in three dimensional systems.
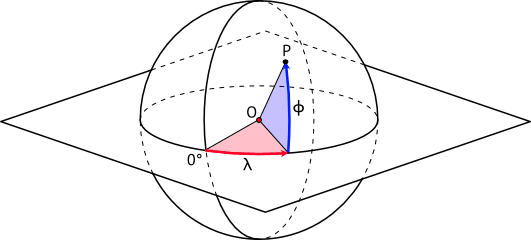
By changing the display options, we can see that the basis vectors are tangent to the. The "radius" of a sphere is the constant distance of its points to the center. The diagram below shows the spherical coordinates of a point P P.

It is the generalization of an ordinary sphere in the ordinary three-dimensional space. In the xy -plane, the right triangle shown in Figure 12.7.1 provides the key to transformation between cylindrical and Cartesian, or rectangular, coordinates. necessary corrections in area/volume differential elements (in this case. The z -coordinate describes the location of the point above or below the xy -plane. In mathematics, an n-sphere or a hypersphere is a topological space that is homeomorphic to a standard n- sphere, which is the set of points in ( n + 1)-dimensional Euclidean space that are situated at a constant distance r from a fixed point, called the center. Converting to spherical coordinates can make triple integrals much easier to. All of the curves are circles: the curves that intersect ⟨0,0,0,1⟩ have an infinite radius (= straight line). In any coordinate system it is useful to define a differential area and a differential volume element. Due to the conformal property of the stereographic projection, the curves intersect each other orthogonally (in the yellow points) as in 4D. This image shows three coordinate directions projected to 3-space: parallels (red), meridians (blue) and hypermeridians (green). A surface of revolution can be de-scribed in cylindrical coordinates as r g(z). Generalized sphere of dimension n (mathematics) 2-sphere wireframe as an orthogonal projection Just as a stereographic projection can project a sphere's surface to a plane, it can also project a 3-sphere into 3-space. The geometrical derivation of the volume is a little bit more complicated, but from Figure 14.5.4 you should be able to see that dV depends on r and, but not on. Evaluate triple integral of xyz dV where E lies between the sphere 1. Area element on surface of sphere (rconstant): da r2 sin dd.


 0 kommentar(er)
0 kommentar(er)
